第3章:ベイズの識別規則_04
リジェクト
事後確率の比が一定以上近しい場合、判断を避けること。
(例)
| C1の事後確率 | C2の事後確率 |
|---|---|
| 0.6 | 0.4 |
⇒この場合、判断を誤る可能性が高いため、あえて判断をしない。
下記のように表す。

(tはリジェクト境界値、Lrがリジェクト領域)
リジェクトの閾値をtとすると、各クラスのリジェクト領域は下記のように表現できる。
| 識別 | C1の事後確率 | C2の事後確率 | リジェクトの閾値 | リジェクトされるパターン(誤差) | リジェクトされるパターン(識別) |
|---|---|---|---|---|---|
 |
0.6 | 0.4 | 0.3 |  |
 |
 |
0.4 | 0.6 | 0.3 |  |
 |
ここから識別規則を整理すると、下記のようになる。


参考までにリジェクト領域を図で表す。

リジェクトする閾値tを下げればりじ、リジェクト率は増加し、認識率は上昇、誤識別率は低下する。
なお、認識率、誤識別率は下記のように定義した。


リジェクト率と認識率、誤識別率の関係性は以下のようなリジェクト-誤識別率曲線を使って表せる。

第3章:ベイズの識別規則_03
ベイズの識別規則による分類と条件付きベイズの誤り率
事後確率が大きい方に分類する
つまり条件付きベイズの誤り率は分類されなかった方の事後確率となる。
| 識別 | 識別の判断 | 事後確率 | 条件付きベイズ誤り率 |
|---|---|---|---|
 |
 |
 |
 |
 |
 |
 |
 |
要するに条件付きベイズの誤り率は下記のように表現できる。

ベイズ誤り率
ベイズ誤り率は領域R1とR2における条件付きベイズ誤り率の期待値として表現される。
(R2に分類された時のC1の事後確率 + R1に分類された時のC2の事後確率)

図で表すと下記のようになる

※参考:積分とは?
関数f(x)を使って囲まれた部分の面積を求めること。
上の例だと、
関数p(x|C1)p(C1)dxで囲まれたR2~の範囲の面積 +
関数p(x|C2)p(C2)dxで囲まれたR1~の範囲の面積
を求めていることになる。
最小損失基準に基づくベイズの識別規則
クラスに分類する際、必ずしも発生する危険性がクラス間で対象であるとは限らない。
(例)
A:健康な人が病気と判断される
B:病気の人が健康と判断される
⇒Bの方がリスクが高い
そこで損失を導入する。(真のクラスがCjのとき、Ciと判断して被る損失)

真 判定
各クラスにおける損失の定義
2クラス分類の場合の損失
| 概要 | 損失 | 損失行列 |
|---|---|---|
| クラスC1と判断することによって被る損失 |  |
 |
| クラスC2と判断することによって被る損失 |  |
 |
損失の期待値

損失による識別(損失が最小のクラスを選ぶ)
| 概要 | 識別の判断 |
|---|---|
 |
 |
 |
 |
その他の識別方法①真の判断を誤ったときの方が真を真と判断するときより損失が大きいと仮定
| 概要 | 識別の判断 |
|---|---|
 |
 |
 |
 |
その他の識別方法②尤度比を利用
| 概要 | 識別の判断 |
|---|---|
 |
 |
 |
 |
損失関数を導入したことによって識別境界が移動する例
(病気を健康と判断した方が損失が大きいと定義する)

第3章:ベイズの識別規則_02
条件付きベイズ誤り率とベイズ誤り率
識別クラスごとの境界が下記のように表される。
| 識別クラス | 識別領域 | 正しく識別される確率 | 条件付きベイズ誤り率 |
|---|---|---|---|
| C1 | R1 | P(C1|x) | P(C2|x) |
| C2 | R2 | P(C2|x) | P(C1|x) |
表を図式化したもの。

つまり条件付きベイズ誤り率は下記の式で表される。

また、ベイズ誤り率は条件付きベイズ誤り率の期待値で表される。

最小損失基準に基づくベイズの識別規則
誤りを起こすことによって生じる損失はクラス間で対称であるとは限らない。
真のクラスがCjのとき、Ciと判断することによって生じる損失を考えてみる。
| No | 数式 | 概要 |
|---|---|---|
| 1 |  |
真がjのときにiと判断することによって生じる損失。前者が判断値、後者が真値。 |
| 2 |  |
真がjのときにiと判断することによって生じる全体への損失(損失×事後確率) |
| 3 |  |
iと判断することによって生じる全体への損失(真がiの場合の損失×事後確率+真がjの場合の損失×事後確率) |
| 4 |  |
クラスijの識別の場合 iと判断することによって生じる全体への損失(真がiの場合の損失×事後確率+真がjの場合の損失×事後確率) jと判断することによって生じる全体への損失(真がiの場合の損失×事後確率+真がjの場合の損失×事後確率) これを損失行列と呼ぶ。 |
④の式を展開すると、下記のようになる。
損失の期待値が最小になるような識別をするには、各微分項が最小になるような領域に判断するのが良い。

となると識別規則は、下記のように表現される。


これを整理すると、下記のようになる。 ←これが一番重要


損失関数によって識別境界がずれる様子。

その他の識別規則の表現方法
識別規則は一般的に間違える方が損失が大きくなるため、Lij > Liiが成り立つ。
これを考慮すると、下記のように表現することもできる。


また尤度比を用いて表現することもできる。


第3章:ベイズの識別規則_01
ベイズの識別規則
観測データをx、識別クラスをCi (i = 1,...,K)としたとき、事後確率が最も大きなクラスに分類する規則のこと。
事後確率は以下の公式で求めることができ、ベイズの定理と呼ばれている。
クラス付き条件確率(=尤度)

事後確率 周辺確率 事前確率
ベイズの識別規則を用いた2クラスの分類
ベイズの識別規則に沿って識別境界を定義すると、クラスCiとクラスCjの事後確率が等しくなるところといえる。

また識別クラスは下記の式で与えられる。なお、周辺確率はどちらのクラスにも共通なため、含めない。

ベイズの識別規則の例
次の表のデータを例にとって、それぞれクラス付き条件確率・同時確率・周辺確率および事後確率を求める。
☆入力データ例

★事前確率と単一変数のクラス付条件確率

★複数変数のクラス付条件確率と同時確率と周辺確率

★事後確率の計算結果
事後確率 = 同時確率/周辺確率

尤度比
ベイズの識別規則による識別境界は2つのクラスの事後確率が等しくなるところで与えられる。
①事後確率 = 同時確率 × 周辺確率
②同時確率 = 事前確率 × クラス付き条件確率
③周辺確率はどちらのクラスにも共通
上記を考慮すると、事前確率とクラス付き条件確率の比率で識別クラスを決定しても良い。


※p(X|C)はクラス付条件確率、P(C)は事前確率
上記を変形してクラス付条件確率の比(尤度比)を用いてクラスを識別することもできる。
事前確率の比が尤度比よりも小さい場合はクラスCiに
事前確率の比が尤度比よりも大きい場合はクラスCjに分類される。


第2章:識別規則と学習法の概要_02
学習データとテストデータの作り方
| No | 手法 | 説明 | その他 |
|---|---|---|---|
| 1 | ホールドアウト法 | 手元のデータを2分割し、一方を学習(PLで表す)に使い、もう一方をテスト(PTで表す)のために取り置いておく方法。 学習データセットを多くする:学習精度は良くなるが、性能評価の精度は悪くなる テストデータセットを多くする:学習制度は悪くなるが、性能評価は良くなる |
誤り率はホールドアウト誤り率と呼ばれ、真の誤り率との間には下記関係が成り立つことが知られている。 学習データセット{ε(PL, PL)} ≦ ε(P, P) ≦ テストデータセット{ε(PL, PT)} |
| 2 | 交差確認法 | データセットをm個に分割する。 m-1個のデータセットで学習を行い。i番目の1つのデータセットで性能評価を行う。 これをm回繰り返す。 |
イメージ図  |
| 3 | 一つ抜き法 | 交差確認法において、データの数とグループの数を等しくした場合を指す。1回実施すればよい。 | 別名ジャックナイフ法とも呼ばれている。 |
| 4 | ブートストラップ法 | N個のデータからN回復元抽出を行いブースストラップサンプルを作成する。 このブースストラップサンプルを学習データにもテストデータにも利用する。 クラスが複数ある場合、それぞれのクラスでブースストラップサンプルを作成するのが一般的。 再代入誤り率の補正のために利用される |
イメージ図 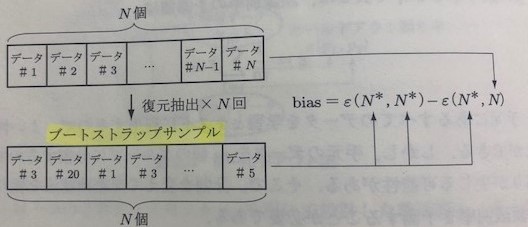 |
※真の誤り率 ・・・ 真の分布p従う学習データを用いて設計し、真の分布pに従うテストデータを用いてテストしたときの誤り率
※再代入誤り率・・・ 学習データを母集団からサンプルし、テストにも同じデータを用いて測定した誤り率
モデル選択
モデル選択とは、テストデータに対する誤り率がもっとも小さくなるようパラメータを調整すること
以下に回帰(関数近似)の例を記述する。
・関数近似によるモデル選択の例
区間[0,1]内で等間隔にサンプルされた11個のサンプルデータから信号成分h(x)を検出することを考える。
信号成分h(x)との近似の良さは平均2乗誤差を用いる。

※関数の重みは学習データセットが決まれば、一意になるため、y(x;D)と表現している。
※y(x;D)→関数近似で算出した特定のデータ、 h(x)→実際のデータの解釈でOK
1つのデータセットで評価することは危険であるため、通常は複数のデータセットを用いて平均2乗誤差を評価し、期待値をとる。

下記の図は3つの学習データセットに対してそれぞれ1次、3次、6次、10次の多項式で近似した例である。
1次式で近似した場合はデータから大きく外れているが、近似した3本の直線はほとんど同じでばらつきは小さい。(バイアスは大きいが、分散は小さい=アンダーフィッティング)
10次式で近似した場合はデータには近似するが、近似した3本の直線はのばらつきは大きい。(バイアスは小さいが、分散は大きい=オーバーフィッティング)
これらの現象を『バイアス・分散トレードオフ』と呼び、汎化能力を決める大きな要因となる。

バイアス項と分散項は(y(x;D) - h(x))^2のデータセットによる期待値Ed{}をとれば、下記の計算式で求めることができる。

上記バイアス・分散トレードオフと汎化能力の関係を図に示すと下記のようになる。
誤差を確認すると3次式以降から徐々に増加しており、ここからも過学習を引き起こしていることが分かる。

今回はモデル選択を説明する際に多項式の次数選択を例に説明したが、識別関数の構成でも同様である。
識別関数は、y = f(x;w) と表すことができる。f() の形やwの要素の数が識別関数の複雑さを決めるため、これらを変えながら交差確認法やブーストラップ法により汎化誤差を推定すればよい。
データの分布に統計モデルを仮定する場合には、解析的に汎化誤差を評価でき、その結果を用いてモデル選択が可能となる。
第2章:識別規則と学習法の概要_01
識別規則の構成法
識別規則は、入力データxからクラスCi = {C1.......Ck}への写像である。
代表的な識別規則は下記の通り
| No | 識別規則 | 概要 | 代表例 |
|---|---|---|---|
| 1 | 事後確率による方法 | パターン空間に確率分布を仮定し、事後確率が最大のクラスに分類する。 | ベイズの最大事後確率法 |
| 2 | 距離による方法 | 入力ベクトルxと各クラスの代表ベクトルとの距離を計算し、一番近い代表クラスに分類する | 最近傍法 |
| 3 | 関数による方法 | 関数f(x)の正負または最大値でクラスを決める | パーセプトロン型学習回路/サポートベクトルマシーン |
| 4 | 決定木による方法 | 識別規則の真偽に応じて次の識別規則を順次適用し、決定木の形でクラスを決める | 決定木 |
教師付き学習
・識別規則
入力データからクラスへの写像をy=f(x)という関数を用いて表現する
パラメータwと入力ベクトルxの線形関数を用いて表現される
y = f(x;w) = W1X1+..........+WdXd = W^tX
・学習の目的
学習データを正しく識別できるWを求めること
・クラスラベル
2クラスの場合
正負の記号を用いて表現する
t = 1
t = -1
3クラス以上の場合
ダミー変数を用いて表現する
t = (0,0,1)^t
t = (0,0,0,0,0,1,0,0,0)^t
→このような符号化方式をK対1符号化と呼ぶ

教師付き学習と線形回帰
教師入力として上記のように{1, 0}の2値ではなく、関数値で与えられるものもある
| 概念 | 説明 |
|---|---|
| 関数近似 | 教師入力として与えられた関数値にできるだけ近似する識別関数f(x)を求めること |
| 線形回帰 | 関数近似のうち、特に線形関数で近似する場合を指す |
汎化能力
| 概念 | 説明 |
|---|---|
| 学習 | 識別関数の出力値と教師データの誤差が最小になるように識別関数のパラメータを調整すること |
| 汎化能力 | 未知のデータに対する識別能力 |
| 汎化誤差 | 学習データとテストデータの性能の差を指す |
第1章:はじめに
パターン認識とは?
| 概念 | 意味 |
|---|---|
| 識別 | 「何か」を判断すること |
| 特徴抽出 | 「有効な特徴」を抽出すること |
| 識別規則 | 「有効な特徴」と「何か」を結びつけること |
| 特徴ベクトル | 抽出された沢山の特徴を並べてベクトルの形にまとめたもの |
| 識別規則 | ある特定のクラスに分類するための識別規則 |
| 汎化能力 | 学習データでない未知のデータに対して正しくクラスを識別できる能力 |
特徴の型
| No | 尺度名 | 定義 | 例 |
|---|---|---|---|
| 1 | 名義尺度 | 分類のための単なる名前。クラスラベル | 名前、住所 |
| 2 | 順序尺度 | 順序関係を表す。比較はできるが加減算などの演算ができない | 大中小、優良可 |
| 3 | 間隔尺度 | 一定の単位で見積もられた量で等間隔性がある。原点があっても「無」ではない。加減算が意味をもつ | 試験の成績、年月 |
| 4 | 比例尺度 | 原点が定まっている量 | 身長、体重、年齢 |

符号化とダミー変数
符号化:クラスに対応する変数のみを1とし、他を0とする
ダミー変数:符号化に用いる2値変数
(例)大中小の符号化
| β1 | β2 | β3 | |
|---|---|---|---|
| 大 | 1 | 0 | 0 |
| 中 | 0 | 1 | 0 |
| 小 | 0 | 0 | 1 |
次元の呪い
・次元の呪い
未知の複雑な関数を学習するために必要なデータが、次元の増加と共に指数関数的に増加すること
特徴量ベクトルはその特徴量の数によってd次元線形空間を張るため、多いほどすさまじい計算量になる。
